TFY4215 Innføring i kvantefysikk
| TFY4215 | |
| Obligatorisk for | Alle våren 2. klasse |
|---|---|
| Forkortelser | Kvante, kvante 1 |
| Laboratorium | Nei |
| Øvinger | Ja, men ikke obligatorisk |
Innføring i kvantefysikk er todelt. I mesteparten av semesteret foreleses kvantemekanikkdelen, som er en første introduksjon til kvantemekanikk. Faget danner grunnlaget for TFY4250 Atom- og molekylfysikk og TFY4205 Kvantemekanikk. De siste tre ukene brukes på kjemisk fysikk, der det man lærte i den første delen anvendes for å gi en dypere forståelse av kjemiske prosesser og molekylers geometri. Her benytter man kvantemekanikk og metoder som Hartree-Fock til å finne energetisk optimal geometri for molekyler.
Laben i faget benytter SPARTAN, et program for å simulere kjemiske prosesser på kvantenivå. Fra våren 2009 er også en av øvingene en dataøving i Matlab der man bruker et program som man får utdelt. Man bruker numeriske beregninger til å bekrefte at ting oppfører seg slik som man har lært, f.eks. at de klassiske vendepunktene i et harmonisk potensial ligger omtrent der krumningen til bølgefunksjonen endres fra positiv til negativ.
Innhold
Kort introduksjon
Å gi en introduksjon til kvantemekanikk bør overlates til foreleser, men jeg forsøker her å legge frem en liten sammenligning mellom kvantemekanisk og klassisk behandling av et svært enkelt problem.
Det gjøres oppmerksom på at teksten ikke er ferdig.
Formulering av problemet
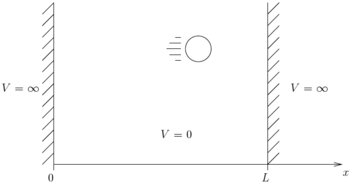
Tenk deg to vegger i avstand <math>L</math> fra hverandre og en perfekt elastisk sprettball med masse <math>m</math> som spretter mellom disse uten påvirking av gravitasjon eller andre ytre krefter. Problemet er av endimensjonal natur. Vi ønsker å se på systemets energi, som her simpelthen er ballens kinetiske energi, og vi ønsker å benytte både en klassisk og en kvantemekanisk betraktning. Det er viktig å merke seg at foruten akkurat idet ballen treffer en vegg og snur, så er dens kinetiske energi den samme. Systemets energi er dermed konstant i tiden, og problemet er ikke tidsavhengig selv om ballen beveger seg i tid. Denne måten å tenke på ser for mange ut til å være problematisk når en først lærer sin grunnleggende kvantemekanikk.
I behandlingen av problemet kommer vi til å fokusere på sprettballens impuls (eller bevegelsesmengde, om en vil), og ikke hastighet, som den fundamentale størrelsen for bevegelse. Klassisk vet vi at det ikke er noe problem å hente en fartsfortolkning fra impulsen, ved bare å dele på massen. Fra kvantemekanikkens ståsted er det nettopp impulsen som opptrer naturlig. Hvorfor dette er tilfelle utdypes nærmere i fagene TFY4230 Statistisk fysikk og TFY4345 Klassisk Mekanikk.
Klassisk behandling
Den klassiske behandlingen av problemet gjør vi i stil med TFY4145 Mekanisk fysikk, selv om TFY4345 Klassisk Mekanikk gjør det på en måte som er langt mer instruktivt når det gjelder kobling mellom klassisk mekanikk og kvantemkekanikk.
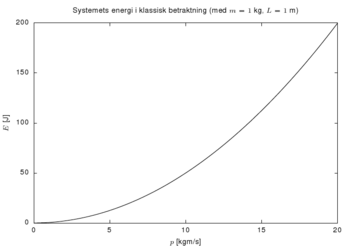
Klassisk er energien <math>E</math> til ballen simpelthen gitt ved
- <math>E = \frac{1}{2}mv^2 = \frac{p^2}{2m}</math>,
hvor <math>v</math> er ballens hastighet og <math>p</math> er dens impuls. Der er ingen andre føringer på energien, og dermed er alle mulige energier mulige (eller alle hastigheter er mulige, alt ettersom hvordan en vil se det).
Kvantemekanisk behandling
På samme måte som Newtons lover danner grunnlaget for den klassiske betrakningen av problemet, danner Schrödinger-ligningen grunnlaget for den kvantemekaniske betrakningen av problemet. Siden problemet er tidsuavhengig, lyder Schrödinger-ligningen
- <math>-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}\psi(x) + V(x)\psi(x) = E\psi(x)</math>,
hvor <math>\psi</math> er systemets bølgefunksjon og <math>E</math> er systemets energi. Bølgefunksjonen er simpelthen en funksjon som løser ligningen over, og som er normalisert til 1, dvs. at integralet av kvadratet av absoluttverdien til funksjonen er 1. Størrelsen <math>\hbar</math> er den reduserte Plancks konstant, også kalt Diracs konstant, som har verdien <math>h/(2\pi)</math>.
Innenfor rammene for behandlingen i denne korte introduksjon, kan Schrödinger-ligningen for problemet slik den er gitt over betraktes som like fundamental som Newtons lover. Det kan være verd å merke seg at Schrödinger-ligningen generelt ikke lyder som over, da ligningen benyttet her simpelthen tilsvarer spesialtilfellet for systemet vårt. Ligningen er avhengig av hva som er systemets Hamilton-operator, men dette skal vi ikke gå inn på her. Det er en gjennomgående trend at et nytt kvantefag innfører minst en ny form av Hamilton-operatoren (f.eks.: spinnsystemer i TFY4250 Atom- og molekylfysikk, spredningsproblemer i TFY4205 Kvantemekanikk og det elektromagnetiske felt i TFY4292 Kvanteoptikk).
Kvantemekanisk modellerer vi veggene som såkalte uendelige potensialbarriærer. Dette er områder der ballens potensielle energi er uendelig, altså hvor den rett og slett ikke kan oppholde seg. Verdien <math>V(x)</math> er dermed 0 for <math>x < L</math> og uendelig for <math>x > L</math>.
For området mellom veggene blir ligningen over
- <math>-\frac{\hbar^2}{2m}\frac{\mathrm{d}^2}{\mathrm{d}x^2}\psi(x) = E_k\psi(x) \quad (1)</math> ,
som jo er en differensialligning med velkjente løsninger <math>\psi_k</math> på formen
- <math>\psi_k (x) = A \sin(kx) + B \cos(kx)</math>.
Utenfor området mellom veggene tvinger den uendelige verdien til V bølgefunksjonen til å være identisk lik 0. Vi påkrever så at <math>\psi_k</math> er kontinuerlig i alle punkter. Dermed får vi kravet
- <math>\psi_k(0) = 0 = \psi_k(L)</math>,
som gir at
- <math>\psi_k (x) = A \sin(kx)</math>,
og
- <math>k = \frac{n\pi}{L}\quad \text{for} \quad n \in \{ 1, 2, 3, \ldots \} </math>.
Ved innsetting i (1) fås
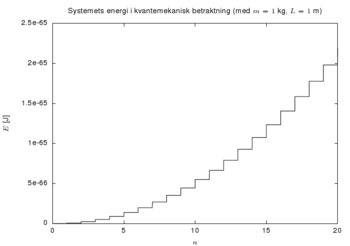
- <math>E_n = \frac{\hbar^2 \pi^2 n^2}{2mL^2} \quad (2)</math>.
Problemet er løst. De mulige energiene for systemet er nettopp de gitt av <math>E_n</math> over. Vi ser at i motsetning til i det klassiske tilfellet, så er ikke alle energier mulige, idet <math>n</math> som gitt over må være et heltall. Vi sier at energispekteret er diskret.
Sammenligning
De to resultatene funnet over kan umiddelbart virke motstridende. Plasserer en en sprettball mellom to plater og rister ivei tilsier jo all erfaring at sprettballen skulle kunne få enhver hastighet, bare en rister riktig. Det er da man skal legge merke til energiskalaen i de to plottene. Energien i den kvantemekaniske betraktningen er 65 størrelsesordner mindre enn i det klassiske tilfellet (hvor energien er av størrelsesorden 1 J). Plottene er for et makroskopisk system, idet massen til ballen er 1 kg, og plateavstanden er 1 m. En må dermed til
- <math>n = \frac{\sqrt{2m}L}{\hbar\pi} = \frac{\sqrt{2}}{\hbar\pi} \approx 4\cdot 10^{33}</math>
for å beskrive det samme energiområdet kvantemekanisk. En skjønner raskt av ligning (2) at avstanden mellom to energitrinn i blir ubetydelig sammenlignet med energien når en lar <math>n</math> bli av en slik størrelse. Dermed sammenfaller (til langt innenfor observasjonsevne) den kvantemekaniske og klassisk beskrivelsen for makroskopiske systemer.
--- Ikke ferdig ---